Monty Hall Problem Simulator

Το πρόβλημα του Monty Hall είναι ένα από τα πιο διάσημα μαθηματικά προβλήματα στο πεδίο της Θεωρίας Πιθανοτήτων:

Σε μια εκπομπή τηλεοπτικού παιχνιδιού ο οικοδεσπότης ζητά από έναν παίκτη να επιλέξει μία από τις τρεις κλειστές πόρτες που βρίσκονται μπροστά από τον παίκτη. Πίσω από τις δύο πόρτες είναι οι κατσίτες και πίσω από μια πόρτα είναι ένα αυτοκίνητο που ο παίκτης μπορεί να κερδίσει όταν παίρνει εκείνη την πόρτα. Αφού ο παίκτης επιλέξει μια πόρτα (η οποία παραμένει κλειστή), ο οικοδεσπότης ανοίγει μια άλλη πόρτα που έχει μια κατσίκα πίσω από αυτό. Ο οικοδεσπότης ζητά από τον παίκτη αν θέλει να μείνει στην πόρτα που επέλεξε στην αρχή ή αν θέλει να μεταβεί στην άλλη κλειστή πόρτα.

Το ερώτημα είναι προφανώς: Εάν ο παίκτης αλλάξει την πόρτα ή παραμείνει στην επιλεγμένη πόρτα;

Πολλοί άνθρωποι μπορούν να πουν ότι δεν έχει σημασία αν ο παίκτης αλλάζει την πόρτα ή όχι, επειδή η πιθανότητα να κερδίσει το αυτοκίνητο είναι 50/50 ούτως ή άλλως. Παρόλο που αυτό φαίνεται εύλογο επειδή υπάρχουν δύο πανομοιότυπες κλειστές πόρτες, είναι λάθος απάντηση.

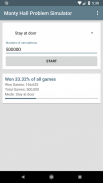
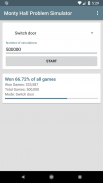
Η σωστή απάντηση είναι ότι η πιθανότητα να κερδίσετε το αυτοκίνητο είναι 67% όταν ο παίκτης αλλάξει την πόρτα και μόνο το 33% όταν ο παίκτης παραμείνει στην πόρτα που επέλεξε πρώτα.

Δεν πιστεύω ότι πληρούνται ακόμα; Απλά κατεβάστε την εφαρμογή και δοκιμάστε την!

Αυτή η εφαρμογή σάς επιτρέπει να προσομοιώνετε αυτόματα το περιγραφόμενο σενάριο παιχνιδιών μέχρι και 5 εκατομμύρια φορές στη σειρά. Μπορείτε να επιλέξετε αν θέλετε ο προσομοιωμένος παίκτης να αλλάζει πάντα την πόρτα ή να παραμένει πάντα στην πόρτα που επιλέγει πρώτα. Αφού η εφαρμογή εξομοιωθεί με τον απαιτούμενο αριθμό παιχνιδιών, σας δίνει ένα στατιστικό στοιχείο που δείχνει πόσα από τα παιχνίδια έχει κερδίσει ο παίκτης. Με αυτόν τον τρόπο μπορείτε να διαπιστώσετε εάν η συσκευή αναπαραγωγής πρέπει ή δεν πρέπει να αλλάξει την πόρτα.